카테고리 없음
[자료구조/C언어] Binary Tree Traversal
JuniTech
2024. 6. 19. 00:02
728x90
1. Traversal
- 트리의 각 노드를 방문하는 과정이라 한다.
- 특정 노드가 있는지 검색할 때 또는 삽입/삭제가 잘 되는지 확인하기 위해 사용된다.
2. Traversal의 종류
- Inorder Traversal : LCR
- 방문 순서 : a left Subtree -> a root node -> a right subtree

Inorder Traversal -
void Inorder(BTreeNode* root) { if (root != NULL) { Inorder(root->left_child); printf("%d ", root->item); Inorder(root->right_child); }
- Preorder Traversal : CLR
- 방문 순서 : a root node -> a left Subtree -> a right subtree

Preorder Traversal -
void Preorder(BTreeNode* root) { if (root != NULL) { printf("%d ", root->item); Preorder(root->left_child); Preorder(root->right_child); } }
- Postorder Traversal : LRC
- 방문 순서 : a left Subtree -> a right subtree -> a root node

Postorder Traversal -
void Postorder(BTreeNode* root) { if (root != NULL) { Postorder(root->left_child); Postorder(root->right_child); printf("%d ", root->item); } }
- Level order Traversal
- 방문 순서 : Level 순서대로 방문한다.
- queue를 사용한다.
- 먼저 레벨 순으로 노드 하나를 삽입후, 노드가 Dequeue될 때 해당 Dequeue되는 노드의 자식 노드 2개를 EnQueue한다.

Level order -
void Levelorder(BTreeNode* root) { Queue queue; if (root == NULL) return; InitQueue(&queue); EnQueue(&queue, root); while (!IsEmpty(&queue)) { root = Peek(&queue); Dequeue(&queue); printf("%d ", root->item); if (root->left_child != NULL) Enqueue(&queue, root->left_child); if (root->right_child != NULL) Enqueue(&queue, root->right_child); } }
3. Tree Traversal의 응용
1. directory size를 다 더해보자!
- 각각의 파일들은 다른 사이즈를 갖고 있고, 각 폴더는 10K의 사이즈를 갖는다.(다, 이진트리이다 보니 디렉토리 파일은 2개 밖에 못만든다.
- post order 방식으로 구현하면 된다.
// Make use of postorder traversal.
int CalDirectorySize(BTreeNode* root) {
int left_size, right_size;
if (root == NULL) return 0;
else {
left_size = CalDiretorySize(root->left_child);
right_size = CalDirectorySize(root->right_child);
return (root->item + left_size + right_size);
}
}
2. Binary Expression Tree를 만들자!
- 우리는 Infix notation(Inorder)이라는 방식이 익숙하다.
- 연산자가 피연산자 사이에 기록되는 방식(Ex. X + Y, (7+4) * 2 - 1 ...)
- 수식 트리(Expression Tree)는 infix 표기법보다 이해하기 쉽다.
-

Expression Tree - 따라서 우리는 다음과 같은 과정을 거쳐서 Expression Tree를 만들 예정이다.

Overall procedure
- Infix notation -> Postfix notation 과정에서는 Stack을 사용하여 Postfix로 변환한다.
- Postfix notation -> Expression tree 과정에서는 Stack을 사용하여 점증적으로 Tree를 만든다.(아래와 같이)


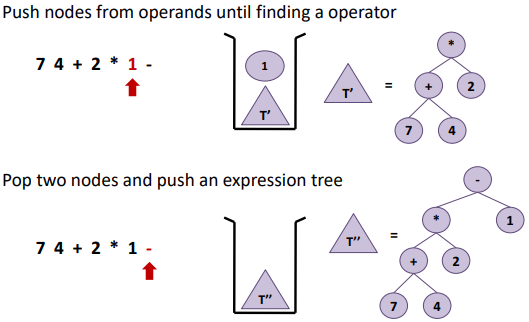
BTreeNode* MakeExpTree(char* exp, int len) { // exp : postfix로 주어진 표기법
Stack stack;
BTreeNode * node, *right_node, *left_node;
InitStack(&stack);
for (int i = 0; i < len; i++) {
// 숫자를 만나면 노드 생성, 연산자를 만나면 오른쪽에 들어갈 노드와 왼쪽에 들어갈 노드를 추출한다.
if ('0' <= exp[i] && exp[i] <= '9') node = CreateNode(exp[i]);
else {
right_node = Peek(&stack), Pop(&stack);
left_node = Peek(&stack), Pop(&stack);
node = CreateNode(exp[i]);
CreateRightSubtree(node, right_node);
CreateLeftSubtree(node, left_node);
}
Push(&stack, node);
}
return Peek(&stack);
}- 아래의 예제와 같이 식을 Tree로 표현하면 Non-leaf node는 operator, leaf node는 operand로 구성되어 있는 것을 확인할 수 있다.

- 이제 위에서 만든 Expression Tree를 계산해보자. 계산하는 과정과 코드는 간단하다. 맨 왼쪽 아래에 있는 Subtree들을 계산하여 나온 값을 왼쪽 자식 노드로 저장한다. 이러한 과정을 반복하면 최종 결과를 얻을 수 있다.



int CalculateExpTree(BTreeNode* root) {
int op1, op2;
if (root == NULL) return 0;
if (root->left_child == NULL && root->right_child == NULL) // Leaf Node=>피연산자=>반환
return root->item;
op1 = CalculateExpTree(root->left_child); // left_child의 피연산자 저장
op2 = CalculateExpTree(root->right_child); // right_child의 피연산자 저장
switch (root->item)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '*': return op1 * op2;
case '/': return op1 / op2;
}
return 0;
}
3. Threaded Binary Tree
- 스레드 이진 트리(Threaded binary tree)는 이진 트리의 한 종류로, 가리키는 곳이 없는 모든 오른쪽 널 포인터(null pointer)를 중위 후속자 노드로 연결하고, 가리키는 곳이 없는 모든 왼쪽 널 포인터를 중위 선행자 노드로 연결한 것이다.
- 재귀적인 Inorder Traversal를 빠르게 할 수 있는 방법이다.
- 순회 방법은 다음과 같다.
- 가장 왼쪽 노드를 찾을 때까지 트리 이동한다.(실선 화살표는 왼쪽 이동을 의미)
- Treaded link 또는 right-side 자식 포인터로 순회한다.(점선 화살표는 오른쪽 이동을 의미)

#include <stdio.h>
typedef int BData;
typedef struct _bTreeNode
{
BData item;
struct _bTreeNode * left_child;
struct _bTreeNode * right_child;
bool isThreaded;
} BTreeNode;
BTreeNode* leftMost(BTreeNode* node)
{
if (node == NULL) return NULL;
while (node->left_child != NULL)
node = node->left_child; // Go to the leftmost node.
return node;
}
void inorder(BTreeNode* node)
{
BTreeNode* cur = leftmost(node);
while (cur != NULL) {
printf("%d ", cur->item);
// If the node is a thread node, go to its inorder successor.
if (cur->isThreaded)
cur = cur->right_child;
else // Go to the leftmost child in a right subtree.
cur = leftmost(cur->right_child);
}
}