| 시간 제한 | 메모리 제한 | 문제 티어 | 정답 비율 |
| 2 초 | 512 MB | 63.255% |
📜 문제
정수 B에 0보다 큰 정수인 N을 곱해 정수 A를 만들 수 있다면, A는 B의 배수이다.
예:
- 10은 5의 배수이다 (5*2 = 10)
- 10은 10의 배수이다(10*1 = 10)
- 6은 1의 배수이다(1*6 = 6)
- 20은 1, 2, 4,5,10,20의 배수이다.
다른 예:
- 2와 5의 최소공배수는 10이고, 그 이유는 2와 5보다 작은 공배수가 없기 때문이다.
- 10과 20의 최소공배수는 20이다.
- 5와 3의 최소공배수는 15이다.
당신은 두 수에 대하여 최소공배수를 구하는 프로그램을 작성 하는 것이 목표이다.
📥입력
한 줄에 두 정수 A와 B가 공백으로 분리되어 주어진다.
50%의 입력 중 A와 B는 1000(103)보다 작다. 다른 50%의 입력은 1000보다 크고 100000000(108)보다 작다.
추가: 큰 수 입력에 대하여 변수를 64비트 정수로 선언하시오. C/C++에서는 long long int를 사용하고, Java에서는 long을 사용하시오.
📤출력
A와 B의 최소공배수를 한 줄에 출력한다.
💡풀이
내가 첫 번째로 푼 풀이는 1부터 증가하는 n을 무한반복을 통해 A와 B로 계속 나누어 나머지가 둘 다 0일 때까지 찾아 최소공배수(Least Common Multiple: LCD)를 구하는 식으로 코드를 작성했다. 해당 코드는 아래와 같다.
import sys
input = sys.stdin.readline
A, B = map(int, input().rstrip().split())
n = 1
while True:
if n % A == 0 and n % B == 0:
print(n)
break
n += 1그러나 위 코드의 시간복잡도는 O(n)이다. 이것보다 더 빠르게 효율적으로 작성할 수 있는 알고리즘이 있다. 바로 유클리드 호제법이다.
https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
유클리드 호제법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 유클리드 호제법(-互除法, Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이다. 호제법이란
ko.wikipedia.org
유클리드 호제법은 최대공약수(Greatest Common Divisor: GCD)를 계산하는 알고리즘이다. (호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.)
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수가 되는 것이다. (증명은 위키 참고)
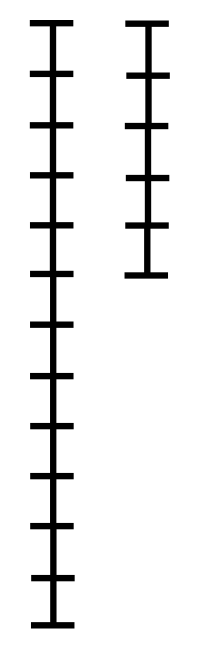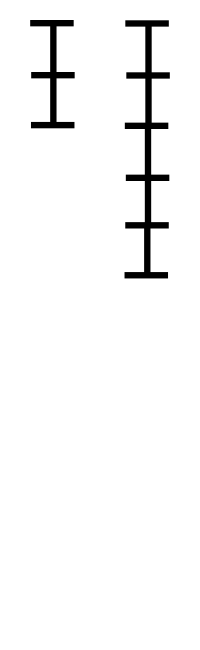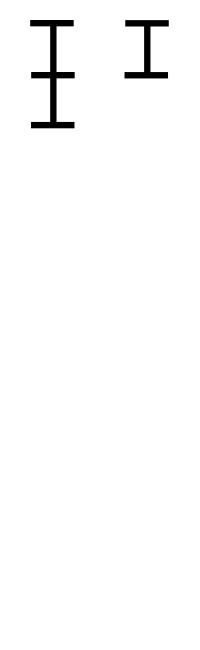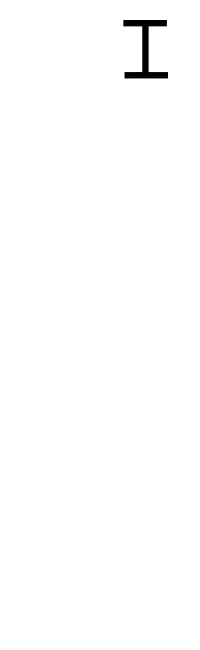
이러한 유클리드 호제법은 최대공약수를 구하는데 시간복잡도가 O(log N)이다.
여기서 또 알아야 할 점은 최대공약수와 최소공배수의 관계이다.
두 자연수 A, B의 최대공약수를 G라고 한다면, A와 B는 다음과 같이 나타낼 수 있다.
A = G x a
B = G x b(단, a, b는 자연수)
이 때 두 자연수 A, B의 곱은 A x B = G x G x a x b 이렇게 되고 최소공배수 L은 정의에 따라 L = G x a x b이므로 최대공약수와 최소공배수의 곱은 두 자연수의 곱과 같아지게 된다.
따라서 위의 식을 정리하면 (A x B) / G = L 이므로 위에 언급한 유클리드 호제법으로 G를 빠르게 구하기만 한다면 L도 바로 구해질 수 있는 것이다.
이러한 바탕으로 작성한 코드는 아래와 같다.
import sys
def gcd(A, B):
while A * B != 0:
if A > B:
A = A % B
else:
B = B % A
return A + B
input = sys.stdin.readline
A, B = map(int, input().rstrip().split())
G = gcd(A, B)
L = int((A * B) / G)
print(L)

'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준/Python] 4134번 : 다음 소수 (0) | 2023.05.28 |
|---|---|
| [백준/Python] 1735번 : 분수 합 (0) | 2023.05.27 |
| [백준/Python] 2501번 : 약수 구하기 (0) | 2023.05.24 |
| [백준/Python] 9506번 : 약수들의 합 (0) | 2023.05.23 |
| [백준/Python] 25206번 : 너의 평점은 (0) | 2023.05.21 |

