1. Sorting 이란?
배열에 데이터를 담게 되면, 가끔은 데이터를 정렬하고 싶을 때가 있을 것이다. 당연히 정렬된 데이터가 그렇지 않은 데이터에 비해 보기도 편하고, 상황에 따라 다루기도 편하기 때문이다.
이처럼 정렬의 중요성은 높기 때문에, 수많은 정렬 알고리즘이 되었다.
우리는 일상적인 정렬 알고리즘에서 시작하여, 개선된 시간의 정렬 알고리즘까지 공부할 것이다.
https://visualgo.net/en/sorting 에서 직관적으로 이해할 수 있다.
Sorting (Bubble, Selection, Insertion, Merge, Quick, Counting, Radix) - VisuAlgo
VisuAlgo is generously offered at no cost to the global Computer Science community. If you appreciate VisuAlgo, we kindly request that you spread the word about its existence to fellow Computer Science students and instructors. You can share VisuAlgo throu
visualgo.net
2. Sorting이 중요한 이유
• 정렬은 검색 및 매칭에 대한 전처리 방법으로 일반적으로 사용되어지고 있다.
– 정렬은 많은 복잡한 문제의 기본 해결책으로 사용된다.
– 대부분의 경우 컴퓨팅 시간의 25% 이상을 정렬하는 데 사용한다.
• 초기 순서 및 목록 크기에 대한 어떤 상황에서도 최적의 알고리즘은 없다. 따라 우리는 몇 가지 기술을 알아야 한다.
– 알고리즘 분석을 위한 기본적인 기술을 이해하기에 좋다.
3. Sorting Algorithms의 카테고리
| Comparison sort | - 비교 정렬 알고리즘은 비교 연산자를 통해 두 요소의 순서를 결정한다. - 2개 이상의 값을 비교하는 연산을 무조건 한다. - Selection sort, Bubble sort, Insertion sort, Quick sort, … |
| Non-comparison sort | - 굳이 원소들의 값을 비교하지 않아도 정렬이 가능하다. - Radix sort, Bucket sort, Counting sort - 선형 정렬 방법이라고도 한다. |
| Internal sort | - 내부 정렬 기법은 정렬되는 자료들이 메인 메모리(주 기억장치)에서 전체적으로 정렬할 수 있을 정도로 작은 경우에 사용된다. - 비교 횟수 최소화 - Selection sort, Bubble sort, Insertion sort, Quick sort, Radix sort, Bucket sort, Counting sort... |
| external sort | - 외부 정렬 기법은 정렬되는 자료들이 너무 커서 메인 메모리(주 기억장치)에 들어갈 수 없을 때 사용된다. - I/O 액세스 횟수 최소화 - ex) disk and SSD - balanced multiway merge sort |
4. Sorting Algorithms의 Stability
- 안정적인 정렬 방법(Stable sorting methods)는 동일한 키로 자료의 순서를 유지하는 방법이다. 키가 동일한 자료의 초기 순서는 변경되지 않는다.
- 쉽게 말해 아래처럼 숫자 순서대로 정렬해도 동일한 key값에 대해서 정렬 전/후 서로의 상대적인 위치가 보존되었 을 때 안정적인 알고리즘(Stable algorithm)이라고 한다.

Stable algorithm VS unstable algorithm
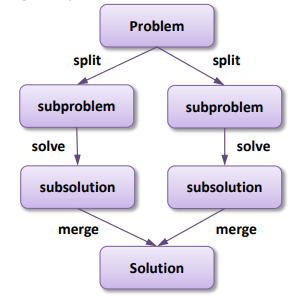
5. Divide & Conquer (D&C) Paradigm (분할 & 정복)
- 먼저 문제를 동일하거나 관련된 유형의 두 개 이상의 하위 문제로 분해하고 하위 문제에 대한 해결책을 원래 문제에 대한 해결책으로 다시 결합하는 과정을 말한다.
- 이후에 설명할 Quick Sort와 Merge Sort에서 쓰이기 때문에 여기서 잠깐 언급한다.
6. Sorting Algorithms 종류
6.1 Selection Sort(선택 정렬)
- 다른 정렬 알고리즘보다 더 일상적인 방법의 알고리즘이다.
- 주 아이디어는 다음과 같다.
- 1. 전체 값 중 가장 작은 값을 찾음
- 2. 해당 값을 맨 첫번째에 배치함
- 3. 첫번째 값을 제외하고 가장 작은 값을 찾아 두번째에 배치함
- 4. 두번째, 세번째, ... n-1번째 값을 제외하고 가장 작은 값을 찾아 정해진 위치에 배치함.
- 시간 복잡도
- Best Case : O(n^2)
- (n - 1) + (n-2) + ... + 2 + 1
- Worst Case : O(n^2)
- 정렬되지 않은 부분에서 최솟값(n) 찾는 것을 매번(n) 해야 하므로
- Best Case : O(n^2)
- Non-stable

void SelectionSort(Data* list, int n) {
int min, temp;
for (int i = 0; i < n - 1; i++) {
min = i;
for (int j = i + 1; j < n; j++) {
// Find an index with the minimum element.
if (list[j] <list[min])
min = j;
}
// Exchange the minimum element and the i-th element.
}
}
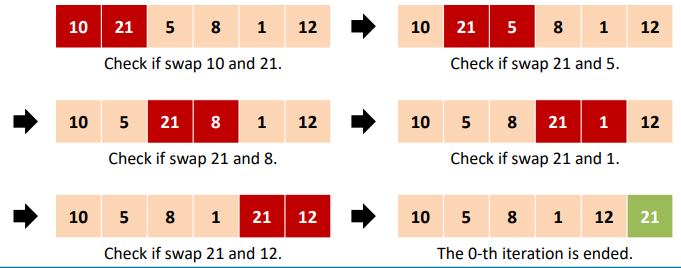
6.2 Bubble Sort(거품 정렬)
- 가장 단순한 정렬 알고리즘이다.
- 주 아이디어는 다음과 같다.
- 1. 첫번째와 두번째 값을 비교한다.
- 2. 두번째와 세번째 값을 비교하고, ... n-1번째와 n번째 값을 비교한다.
- 이 과정에서 순서가 맞지 않은 값을 서로 교환해준다. 이런 절차를 정렬이 될 때 까지 반복한다.
- 코드를 작성하는 것은 어렵지 않지만, 상당히 비효율적인 알고리즘이기 때문에, 성능이 다른 알고리즘에 비해 좋지 않다는 단점이 있다.
- 시간 복잡도
- Best case : O(n^2)
- 정렬이 되어 있어도 인접한 애들끼리 비교를 n번만큼해서 총 n번 반복하므로
- Worst case : O(n^2)
- Best case : O(n^2)
- Stable
void BubbleSort(Data* list, int n) {
int temp;
for (int i = n - 1; i > 0; i--) {
for (int j = 0; j < n; j++)
{
// Compare each pair of adjacent items.
if (list[j] > list[j + 1]) {
// Swap if they are in the wrong order.
SWAP(list[j], list[j + 1], temp);
}
}
}
}
6.3 Insertion Sort(삽입 정렬)
- 삽입정렬은 앞에서부터 순서대로 보면서 앞에 있는 모든 원소가 정렬이 되어 있다는 가정 하에서 현재 원소의 위치를 적절하게 집어넣는 정렬이다.
- 시간 복잡도
- Best Case : O(n)
- (역)정렬이 되어있다면 매 검사마다 1번씩만 해도 됨.
- Worst Case : O(n^2)
- Best Case : O(n)
- Stable

void InsertionSort(Data* list, int n) {
int j, key;
for (int i = 1; i < n; i++) { // 0번째 원소는 굳이 할 필요 X)
key = list[i]; // Choose the i-th element.
for (j = i - 1; j >= 0; j--) {
// 만약 현재 원소 key가 비교하는 원소 list[j]보다 작으면, list[j]를 오른쪽으로 한 칸 이동시킨다.
if (key < list[j])
list[j+1] = list[j];
else break;
}
// 만약 key가 list[j]보다 크거나 같다면, 올바른 위치를 찾은 것이므로 내부 루프를 중단하고 key를 j+1 위치에 삽입한다.
list[j+1] = key;
}
}
6.4 Quick Sort(퀵 정렬)
- 1959년 토니 호어에 의해 발명된 정렬이다.
- 분열과 정복(D&C) 패러다임을 기반으로 한다.
- 시간 복잡도
- average case : O(nlogn)
- worst case : O(n^2)
- Pivot을 극도로 치우쳐진 경우로 선택하면 더 나쁜 경우가 발생한다.
– 빠른 정렬의 시간 복잡성은 주로 피벗 선택에 따라 달라진다.
- Pivot을 극도로 치우쳐진 경우로 선택하면 더 나쁜 경우가 발생한다.
- 전체적인 절차는 다음과 같다.
- Pivot 선택: 목록에서 피벗이라고 하는 요소를 선택한다.
- Partitioning: 피벗을 사용하여 목록 순서를 바꾼다.
- 피벗보다 작은 요소가 피벗 앞에 온다.
- 피벗보다 큰 요소는 피벗 다음에 온다.
- 위의 단계를 하위 목록에 재귀적으로 적용한다.
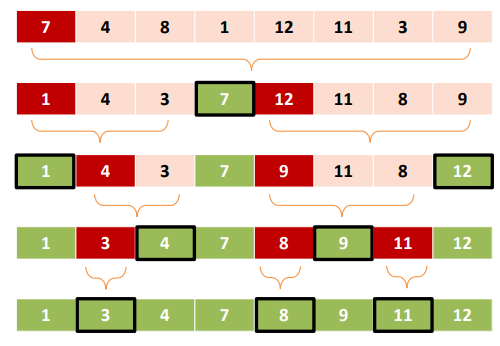
Partitioning
- 위 단계를 하기 위해서 Partitioning을 해야 한다.
- 목록에서 피벗을 선택한다.
- 일반적으로 가장 왼쪽에 있는 요소가 피벗으로 선택된다.
- 사실 맨 왼쪽 말고 랜덤하게 pivot을 고른다던지, 끝값, 처음값, 중간값 중 중간값을 고르는 것이 좋은 pivot 선택 방법일 수 있다.
- low 변수와 high 변수를 사용한다.
– low: L[low]가 피벗보다 작으면 오른쪽 요소로 이동한다.
– high: L[high]가 피벗보다 크면 왼쪽 요소로 이동한다.
– L[ low]과 L[high] 두 요소를 SWAP한다. - 낮은 것과 높은 것이 교차되면 파티션 분할을 중지한다.
– L[left]과 L[high] 두 요소를 스왑합니다.

int Partition(Data* list, int left, int right) {
int pivot = list[left], temp;
int low = left + 1, high = right;
while(1) {
while(low < right && list[low] < pivot)
low++; // Move low until pivot < L[low]
while(high > left && list[high] >= pivot)
high--; // Move high until pivot >= L[low]
if (low < high)
// Swap list[low] and list[high].
SWAP(list[low], list[high], temp);
return high; // return the pivot position.
}
}
void QuickSort(Data* list, int left, int right) {
if (left < right) {
// The mid refers to the pivot position.
int mid = Partition(list, left, right);
// All elements are less than the pivot.
QuickSort(list, left, mid - 1);
// All elements are greater than the pivot.
QuickSort(list, mid + 1, right);
}
}
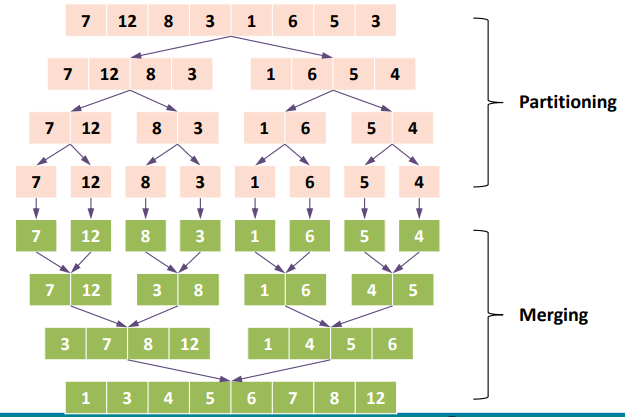
6.5 Merge Sort(병합 정렬)
- Quick Sort의 치우쳐진 경우와는 반대로, Merges Sort는 반반으로 나누어서 쪼개어서 해결하는 방법이다.
- 병합 정렬은 배열의 길이가 1개가 될 때 까지 재귀적으로 쪼개기 → 쪼갠 배열을 합쳐가며 정렬된 배열로 만들기 라는 과정을 거치게 된다.
- 시간 복잡도
- Average case / Worst case : O(nlogn)
- Stable
- D&C 패러다임을 활용한다. 전반적인 절차를 정리하면 다음과 같다.
- Partitioning
– Divide: 목록을 반으로 나눕니다.
– Conquer : 두 개의 하위 목록을 정렬한다. - Merge
– Combine : 정렬된 두 개의 부표를 하나의 목록으로 병합한다.
– 위의 단계를 하위 목록에 재귀적으로 적용한다.
- Partitioning
- 다시 하나의 리스트로 병합할 때
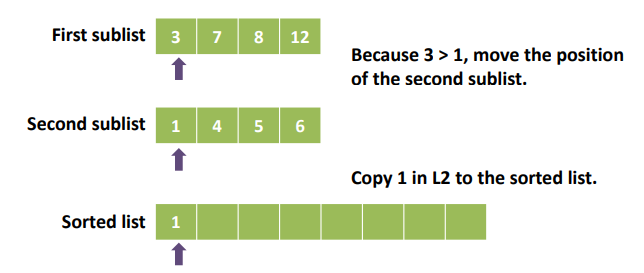
- List1과 List2의 두 요소를 순차적으로 비교한다.
- List1의 요소가 List2의 요소보다 작거나 같으면 List1의 next 위치로 이동한다.
- List1의 원소가 List2의 원소보다 크면 List2의 next 위치로 이동한다.
- List1과 List2의 두 요소를 순차적으로 비교한다.




void Merge(Data* list, int left, int mid, int right) {
int sorted[MAX_SIZE];
int first = left, second = mid + 1, i = left;
// Merge two lists by comparing elements in sequence.
while (first <= mid && second <= right) {
if (list[first] <= list[second])
sorted[i++] = list[first++];
else
sorted[i++] = list[second++];
}
// For remaining items, add them in sequence.
if (first > mid)
for (int j = second; j <= right; j++)
sorted[i++] = list[j];
else
for (int j = first; j <= mid; j++)
sorted[i++] = list[j];
// Copy the sorted list to the list.
for (int j = left; j <= right; j++)
list[j] = sorted[j];
}
void MergeSort(Data*list, int left, int right) {
if (left < right) {
int mid = (left + right) / 2; // Equal partitioning
MergeSort(list, left, mid); // Sorting sublists
MergeSort(list, mid + 1, right); // Sorting sublist
Merge(list, left, mid, right); // Merging two sublists
}
}
- Recursive Version 말고 Iterative Version의 Merge Sort 코드는 다음과 같다.
void IterMergeSort(Data* list, int n) {
// Merge subarrays in bottom up manner. First merge subarrays of size 1
// to create sorted subarrays of size 2, then merge subarrays of size
// 2 to create sorted subarrays of size 4, and so on.
// 쪼개고 바로 합친다는 점에서 Recursive와 차이점이 있다.
// Recursive는 다 쪼개고 난뒤 합친다.
for (int size = 1; size <= n - 1; size = 2* size) {
// Pick starting point of different subarays of current size
for (int left_start = 0; left_start < n - 1; left_start += 2 * size){
// Find ending point of left subarray.
// mid + 1 is starting point of right
int mid = left_start + size - 1;
int right_end = MIN(left_start + 2 * size - 1, n - 1);
// Merge Subarrays arr[left_start...mid] & arr[mid+1...right_end]
Merge(list, left_start, mid, right_end);
}
}
}- 설명하자면 Iterativer 버전은 Recursive 버전과 다르게 매개변수가 "리스트" (list), "리스트 길이" (n) 2가지만 주어진다. 즉, 길이가 n인 list를 길이가 1인 sublist n개가 있다고 간주해보자.
- 정렬 단계는 다음과 같다.
- 각 i 번째 반복마다 길이가 i 인 sublist 를 병합 (merge) 하는 과정이라 생각하면 된다.
- 첫번째, 각 sublist 들을 쌍으로 병합하여 크기가 2*1 이고, n/2 개인 정렬된 sublist들을 만든다. ( Merge() 함수를 호출하면 정렬해서 병합하는 과정은 recursive때와 동일하게 동작합니다.)
- 두번째, n/2 개의 sublst 들에 대해 길이가 2*2 인 n/4 개의 정렬된 sublist를 만든다.
- ...
- 각각의 반복에서 병합할때마다 sublist 개수는 반으로 줄어든다. sublist가 하나가 남을때까지 반복한다.
- 각 i 번째 반복마다 길이가 i 인 sublist 를 병합 (merge) 하는 과정이라 생각하면 된다.

7. Sorting 알고리즘 비교
| Algorithm | Best | Average | Worst |
| Selection sort | O(n^2) | O(n^2) | O(n^2) |
| Bubble sort | O(n^2) | O(n^2) | O(n^2) |
| Insertion sort | O(n) | O(n^2) | O(n^2) |
| Quick sort | O(nlog n) | O(nlog n) | O(n^2) |
| Merge sort | O(nlog n) | O(nlog n) | O(nlog n) |
| Heap sort | O(nlog n) | O(nlog n) | O(nlog n) |
- Insertion sort
- Best case : O(n)
- 작은 자료들을 정렬하는데 유용
- Quick sort
- Best in average case
- Worst case : O(n^2)
- Merge sort
- Best in the worst case : O(nlog n)
- 위 sorting algorithms의 비교를 통해서 다음과 같은 예제를 내릴 수 있다.(n : 원소의 개수)
- Insertion sort는 n < 20일 때 가장 빠르다.
- Quick sort는 20 < n < 45일 때 가장 빠르다.
- Merge sort는 n이 엄청 클 때 가장 빠르다.
- 위 내용을 토대로 QuickSort를 아래와 같이 코드를 작성할 수 있다.
void QuickSort(Data* list, int left, int right) {
if (left < right) {
// The mid refers to the pivot position.
int mid = Partition(list, left, right);
// All elements are less than the pivot.
if (mid - left < 20) // 원소의 개수가 20개 이하일 때, 삽입정렬이 가장 빠르다.
InsertionSort(list, left, mid - 1);
else // 원소의 개수가 20개 그 이상이면 QuickSort로 !
QuickSort(list, left, mid - 1);
// All elements are greater than the pivot.
if (right - mid < 20)
InsertionSort(list, left, mid - 1);
else
QuickSort(list, left, mid - 1);
}
}
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조/C언어] 우선순위 큐 & 힙 (0) | 2024.06.18 |
|---|---|
| [자료구조/C언어] Hash (0) | 2024.06.18 |
| [자료구조/C언어] AVL Tree (0) | 2024.06.18 |
| [자료구조/C언어] Red-Black Tree | 2-3 Tree | B-Tree (0) | 2024.06.18 |
