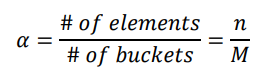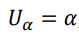목차
728x90
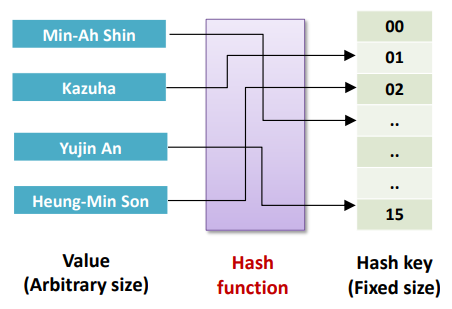
1. Hash란?
- 임의의 크기의 값을 고정된 크기의 값으로 매핑하는 데 이때 해시 함수를 사용한다.
- key 와 values 를 가진다.
- 검색 속도를 O(1)으로 만들기 위해 사용된다.
2. 좋은 Hash Function은?
- 해시 함수는 원소들이 균일하게 분포될 수 있을 만큼 충분히 골고루 분포되어야 한다.
– 해시 함수는 편향되지 않아야 한다.
– 요소에 모든 비트를 사용해야 한다 - 범용 해시 함수
– 𝑏 버킷이 있는 경우 ℎ (𝑥) = 𝑖 확률은 모든 버킷에 대해 1/𝑏 이다.(이러한 확률을 가지고 있어야 굿)
– 요소 𝑥는 1/𝑏 확률로 모든 버킷 𝑖에 넣을 수 있다. - Hash Function으로는 Mid-square, Division, and Folding을 사용한다.
2.1. Hash Function 종류
2.1. Mid-square (middle of square)
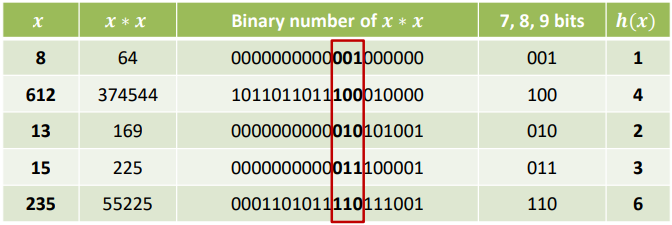
- ℎ(𝑥): x * x의 중간에서 𝑟 비트를 가져온다.
- 2^r 개의 buckets 들이 생성된다.
- Example) h(x)는 7*7의 7번째 비트로부터 3개의 비트를 가지고 오는 해시 함수이다.
-
![]()
Mid-square
2.2. Division(modular)
- ℎ(𝑥) = 𝑥 𝑚𝑜𝑑 𝑀, 여기서 𝑀는 테이블 크기를 의미한다.
▪ 버킷 주소 범위: 0 ~ 𝑀 - 1 - 𝑀의 선택은 매우 중요하다.
▪ 거듭제곱 2에 너무 가깝지 않도록 소수 𝑀을 선택하자.
2.3. Folding: shift folding
- 지정된 키 k는 각각 필요한 주소와 길이가 동일한 𝑘1, 𝑘2, …, 𝑘𝑛로 분할되는 해시 함수이다.
- Example: ℎ(94034) = ℎ(94) + ℎ(03) + ℎ(4) = ℎ(101)
3. 해시 충돌 & 해결책
- 해시 함수 ℎ(𝑥)가 주어졌을 때, 두 개의 서로 다른 키 𝑖 및 𝑗의 값이 동일할 수 있다.
- ℎ(𝑖) = ℎ(𝑗) 와 같이 동일한 상황을 '충돌'났다고 말한다.
- 해결책 : open addressing, closed addressing
| Open Addressing (충돌 발생했을 때 충돌 난 요소를 다른 버킷에 쓸 수 있도록 허용) |
Linear Probing | * bucket이 가득 차면 빈 bucket 을 찾을 때까지 다음 bucket 으로 이동하는 해결책이다. * ex) h(x) = x mod 10  * 그러나 이 문제는 Clustering과 Coalescing이 발생하는 문제가 생긴다. (ex. 나머지가 다 2면 해시함수의 의미가 없어짐->2개 이상의 그룹이 서로 얽히고 얽혀짐->해시함수 기능 저하) – Clustering: elements are grouped – Coalescing: two adjacent groups are merged |
| Quadratic probing | * ℎ (𝑥) + inc ∗ inc mod M 순서로 빈 버킷을 검색하는 해결책이다. * ex) h(x) = x mod 10 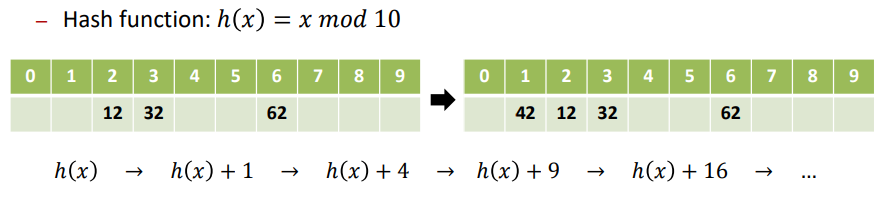 * Clustering과 Coalescing 문제를 피할 수 있는 좋은 해결책이다. |
|
| Double Hashing | * collision이 발생할 경우 다른 해싱 기능을 사용하는 해결책이다. * Rehashing이라고도 부른다. * Quadratic probing과 다른 점 : 충돌 발생시 Double Hashing은 다른 hash 함수를 사용하게 된다. - ex) 단계: 𝑖𝑛𝑐 ∗ 𝑖𝑛𝑐 → 𝑖𝑛𝑐 ∗ ℎ_2(𝑥) 충돌 발생시 ℎ_1(𝑥) + 𝑖𝑛𝑐 ∗ ℎ_2(𝑥) 𝑚𝑜𝑑 M 순서로 빈 버킷을 검색한다. * 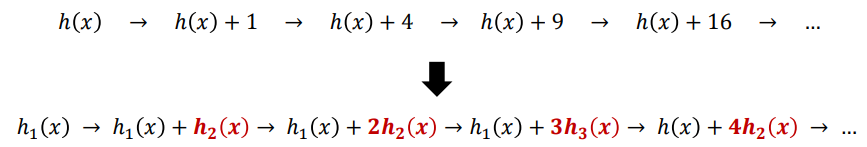 |
|
| Random probing | * 이름대로 랜덤한 위치를 찾으며 empty 원소를 찾을 때까지 조사하는 방식이다. | |
| Closed Addressing (충돌 발생했을 때 충돌 난 요소를 해당 버킷 내에서 해결) |
Chaining | * 각 bucket에 대해 충돌난 요소의 linked list를 사용하는 해결책이다. |
4. Hashing의 성능 분석
- 해시함수는 Loading factor 𝛼 로 성능 분석한다.
- Loading factor는 해시 테이블이 얼마나 가득 찼는지를 측정하는 지표이다.
![]()
Loading factor
- Loading factor는 해시 테이블이 얼마나 가득 찼는지를 측정하는 지표이다.
- 𝑈𝛼: 존재하지 않는 요소에 대한 검색 / 𝑆𝛼: 기존 요소들에 대한 검색
| 𝑈𝛼 | 𝑆𝛼 | |
| Linear probing | 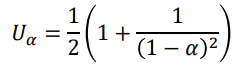 |
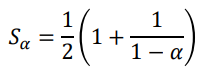 |
| Chaining | 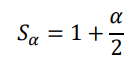 |
- 증명은 확통으로 할 수 있다.
5. Hashing의 시간복잡도
- 일반적으로 hashing은 검색하는데 있어서 아주 좋은 방법이다.
![]()
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조/C언어] 우선순위 큐 & 힙 (0) | 2024.06.18 |
|---|---|
| [자료구조/C언어] Sorting Algorithms (정렬 알고리즘) (0) | 2024.06.18 |
| [자료구조/C언어] AVL Tree (0) | 2024.06.18 |
| [자료구조/C언어] Red-Black Tree | 2-3 Tree | B-Tree (0) | 2024.06.18 |
728x90
1. Hash란?
- 임의의 크기의 값을 고정된 크기의 값으로 매핑하는 데 이때 해시 함수를 사용한다.
- key 와 values 를 가진다.
- 검색 속도를 O(1)으로 만들기 위해 사용된다.

2. 좋은 Hash Function은?
- 해시 함수는 원소들이 균일하게 분포될 수 있을 만큼 충분히 골고루 분포되어야 한다.
– 해시 함수는 편향되지 않아야 한다.
– 요소에 모든 비트를 사용해야 한다 - 범용 해시 함수
– 𝑏 버킷이 있는 경우 ℎ (𝑥) = 𝑖 확률은 모든 버킷에 대해 1/𝑏 이다.(이러한 확률을 가지고 있어야 굿)
– 요소 𝑥는 1/𝑏 확률로 모든 버킷 𝑖에 넣을 수 있다. - Hash Function으로는 Mid-square, Division, and Folding을 사용한다.
2.1. Hash Function 종류
2.1. Mid-square (middle of square)
- ℎ(𝑥): x * x의 중간에서 𝑟 비트를 가져온다.
- 2^r 개의 buckets 들이 생성된다.
- Example) h(x)는 7*7의 7번째 비트로부터 3개의 비트를 가지고 오는 해시 함수이다.
-
![]()
Mid-square
2.2. Division(modular)
- ℎ(𝑥) = 𝑥 𝑚𝑜𝑑 𝑀, 여기서 𝑀는 테이블 크기를 의미한다.
▪ 버킷 주소 범위: 0 ~ 𝑀 - 1 - 𝑀의 선택은 매우 중요하다.
▪ 거듭제곱 2에 너무 가깝지 않도록 소수 𝑀을 선택하자.
2.3. Folding: shift folding
- 지정된 키 k는 각각 필요한 주소와 길이가 동일한 𝑘1, 𝑘2, …, 𝑘𝑛로 분할되는 해시 함수이다.
- Example: ℎ(94034) = ℎ(94) + ℎ(03) + ℎ(4) = ℎ(101)
3. 해시 충돌 & 해결책
- 해시 함수 ℎ(𝑥)가 주어졌을 때, 두 개의 서로 다른 키 𝑖 및 𝑗의 값이 동일할 수 있다.
- ℎ(𝑖) = ℎ(𝑗) 와 같이 동일한 상황을 '충돌'났다고 말한다.
- 해결책 : open addressing, closed addressing
| Open Addressing (충돌 발생했을 때 충돌 난 요소를 다른 버킷에 쓸 수 있도록 허용) |
Linear Probing | * bucket이 가득 차면 빈 bucket 을 찾을 때까지 다음 bucket 으로 이동하는 해결책이다. * ex) h(x) = x mod 10  * 그러나 이 문제는 Clustering과 Coalescing이 발생하는 문제가 생긴다. (ex. 나머지가 다 2면 해시함수의 의미가 없어짐->2개 이상의 그룹이 서로 얽히고 얽혀짐->해시함수 기능 저하) – Clustering: elements are grouped – Coalescing: two adjacent groups are merged |
| Quadratic probing | * ℎ (𝑥) + inc ∗ inc mod M 순서로 빈 버킷을 검색하는 해결책이다. * ex) h(x) = x mod 10  * Clustering과 Coalescing 문제를 피할 수 있는 좋은 해결책이다. |
|
| Double Hashing | * collision이 발생할 경우 다른 해싱 기능을 사용하는 해결책이다. * Rehashing이라고도 부른다. * Quadratic probing과 다른 점 : 충돌 발생시 Double Hashing은 다른 hash 함수를 사용하게 된다. - ex) 단계: 𝑖𝑛𝑐 ∗ 𝑖𝑛𝑐 → 𝑖𝑛𝑐 ∗ ℎ_2(𝑥) 충돌 발생시 ℎ_1(𝑥) + 𝑖𝑛𝑐 ∗ ℎ_2(𝑥) 𝑚𝑜𝑑 M 순서로 빈 버킷을 검색한다. * 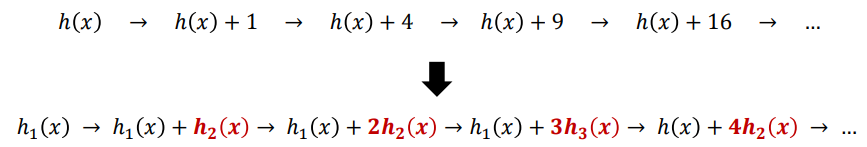 |
|
| Random probing | * 이름대로 랜덤한 위치를 찾으며 empty 원소를 찾을 때까지 조사하는 방식이다. | |
| Closed Addressing (충돌 발생했을 때 충돌 난 요소를 해당 버킷 내에서 해결) |
Chaining | * 각 bucket에 대해 충돌난 요소의 linked list를 사용하는 해결책이다. |
4. Hashing의 성능 분석
- 해시함수는 Loading factor 𝛼 로 성능 분석한다.
- Loading factor는 해시 테이블이 얼마나 가득 찼는지를 측정하는 지표이다.
![]()
Loading factor
- Loading factor는 해시 테이블이 얼마나 가득 찼는지를 측정하는 지표이다.
- 𝑈𝛼: 존재하지 않는 요소에 대한 검색 / 𝑆𝛼: 기존 요소들에 대한 검색
| 𝑈𝛼 | 𝑆𝛼 | |
| Linear probing | 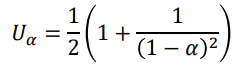 |
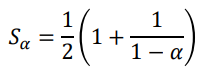 |
| Chaining | 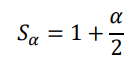 |
- 증명은 확통으로 할 수 있다.
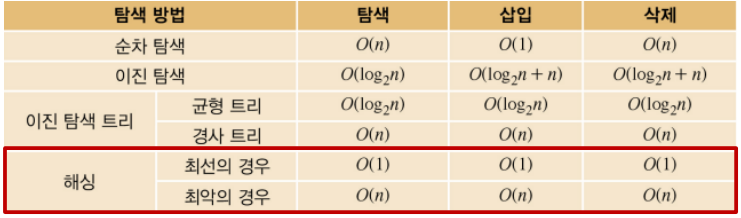
5. Hashing의 시간복잡도
- 일반적으로 hashing은 검색하는데 있어서 아주 좋은 방법이다.
![]()
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조/C언어] 우선순위 큐 & 힙 (0) | 2024.06.18 |
|---|---|
| [자료구조/C언어] Sorting Algorithms (정렬 알고리즘) (0) | 2024.06.18 |
| [자료구조/C언어] AVL Tree (0) | 2024.06.18 |
| [자료구조/C언어] Red-Black Tree | 2-3 Tree | B-Tree (0) | 2024.06.18 |