728x90
1. What is Priority Queue(우선순위 큐란)?
- Queue(FIFO) 와 유사하다. 여기서 각 요소에 우선 순위가 있다는 것이 바로 Priority Queue라 한다.
2. How to implement a priority queue (어떻게 우선순위 큐를 구성할 것인가)?
- Heap-based implementation (우리는 이 방식을 쓸 것이다.)
| 우선순위 큐 구성 방식 | 특징 |
| a unsorted array/linked list |
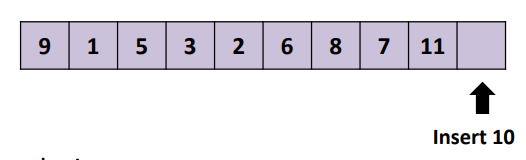 |
| a sorted array/linked list |
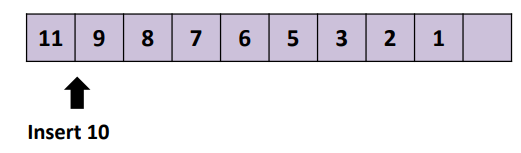 |
| Heap (우리는 이 방식으로 쓸 것이다.) |
|
3. What is Heap(힙이란?)
- 보통 max heap을 의미한다.
- Complete binary tree 이다.
- 따라서 n개의 노드들이 있을 때 높이는 O(log_2(n))이다.
- level i에서 2^i개의 노드들이 존재한다.(단, last level에서는 제외)
- 루트 값은 항상 트리에서 최댓값이다.
- Subtrees들도 항상 힙을 이룬다. => key(parent) >= key(child)

4. Heap 구현 & 코드
- 배열을 기반으로 구현할 것이다. (힙은 완전이진트리이므로, 각 노드들은 연속적으로 인덱스가 있을 것이다.)
- node의 index가 x라면 왼쪽 자식 노드의 인덱스는 2x, 오른쪽 자식 노드의 인덱스는 2x + 1 이다.
- 위와 같은 인덱스를 구현하기 위해 root 노드의 인덱스는 1부터 시작해야 한다.
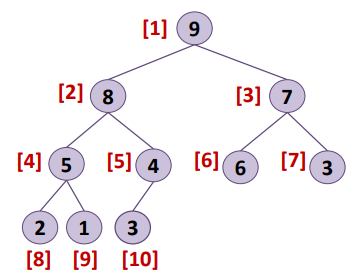

// Get a parent index for a given index.
int GetParent(int idx) {
reuturn idx / 2;
}
// Get a left child index for a given index.
int GetLChild(int idx) {
return idx * 2;
}
// Get a right child index for a given index.
int GetRChild(int idx) {
reuturn idx * 2 + 1;
}- Insertion할 때, 일단 무조건 삽입할 노드를 Tree의 마지막에 놓고, 그 위 부모(조상)들이랑 값을 비교한다. 비교해서 Heap 조건이 성립하면 삽입할 자리 그대로 넣고, 삽입할 노드가 삽입 위치의 부모노드보다 값이 크다면 해당 부모와 위치를 바꾼다.
void Insert(Heap *pheap, Data data, int priority)
{
HNode newNode;
int idx = pheap->num + 1; // last node
if (IsFull(pheap)) exit(1);
// Compare the new node with its parent.
while (idx > 1) { // 부모 -> 부모 -> ... -> root까지 비교
int parent = GetParent(idx); // 현재 노드 넣는 위치의 부모 인덱스를 불러온다.
if (priority > pheap->items[parent].priority) { // 우선순위 비교 -> 자식이 높다면 값 SWAP!
pheap->items[idx] = pheap->items[parent];
idx = parent;
}
else break;
}
// 삽입할 위치를 찾았으면 노드를 추가한다.
newNode.data = data;
newNode.priority = priority;
pheap->items[idx] = newNode;
pheap->num++;
}- Deletion할 때, Max Heap이든 Min Heap이든 무조건 root(최댓값 또는 최솟값)을 삭제하는 것이다.
- 먼저 Tree의 마지막 인덱스에 있는 노드를 root 노드로 옮긴다.(고민하지 말고 일단 올려!)
- 그 다음, root 노드로 옮긴 노드를 아래 방향으로 Heap 조건이 맞는지 비교 check한다. 이 때 비교할 자식노드(Left Child, Right Child) 중 가장 큰 노드와 비교한다.
- 그렇게 해서 자리를 찾으면 거기에 값을 넣으면 된다.
Data Delete(Heap *pheap)
{
Data max = pheap->items[1].data; // root 노드 데이터
HNode last = pheap->items[pheap->num]; // 가장 마지막 노드 데이터
int parent = 1, child;
// Compare the root with its child nodes.
while (child = GetHighPriorityChild(heap, parent)) {
// last node가 root node로 갔을 때 거기에서 우선순위가 높은 자식과 비교-> 자식이 더 크면 그 자식을 부모 노드로 변경
if (last.priority < pheap->items[child].priority) {
pheap->items[parent] = pheap->items[child];
parent = child; // parent 변수는 child index를 받고 다시 그 위치에서 자식들 우선순위 비교해서 자리를 찾는다.
}
}
else break;
}
// 값이 고쳐진 parent(index)에 해당되는 items 위치에 last를 넣는다.
pheap->items[parent] = last;
pheap->num--; // size 1 감소
}
// 자식들 간의 우선순위 비교해서 더 높은 자식의 index 반환
int GetHighPrioityChild(Heap *pheap, int idx)
{
if (GetLChild(idx) > pheap->num) return 0; // No child nodes exist.
else if (GetLChild(idx) == pheap->num) // Exist a left child only.
return GetLChild(idx);
else { // Choose a child node with the highest priority.
int left = GetLChild(idx), right = GetRChild(idx);
if (pheap->items[left].priority > pheap->items[right].priority)
return left;
else
return right;
}
}
- https://visualgo.net/en/heap 을 참고하자.
Binary Heap (Priority Queue) - VisuAlgo
VisuAlgo is generously offered at no cost to the global Computer Science community. If you appreciate VisuAlgo, we kindly request that you spread the word about its existence to fellow Computer Science students and instructors. You can share VisuAlgo throu
visualgo.net
5. Priority Queue 구현 & 코드
- Heap 기반으로 구현된다.
#include "Heap.h"
typedef Heap PQueue;
void InitPQueue(PQueue* ppqueue);
bool IsPQEmpty(PQueue* ppqueue);
bool IsPQFull(PQueue* ppqueue);
// Insert an item to the priority queue.
void Enqueue(PQueue *ppqueue, Data data, int priority); // 인자로 priority까지 있어야 우선순위 뭐가 높은지 알 수 O
// Delete an item to the priority queue.
Data Dequeue(PQueue *ppqueue); // 우선순위 가장 높은걸(root node) 빼기로 약속함.
void InitPQueue(PQueue* ppqueue) {
InitHeap(ppqueue);
}
bool IsPQEmpty(PQueue* ppqueue) {
return IsEmpty(ppqueue);
}
bool IsPQFull(PQueue* ppqueue) {
return IsFull(ppqueue);
}
void Enqueue(PQQueue *ppqueue , Data data, int priority) {
Insert(ppqueue, data, priority);
}
Data Dequeue(PQueue* ppqueue) {
return Delete(ppqueue);
}
6. Heap Sort
- Max Heap을 사용해서 정렬하는 기법이다.
- Step1. Heap에다가 각 요소들을 삽입한다.
- Step2. Heap으로부터 순차적으로 모든 요소들을 추출해 배열에 저장한다.

void HeapSort(Data a[], int n) {
Heap heap;
InitHeap(&heap);
// Insert all elements to the heap.
for (int i = 0; i < n; i++)
Insert(&heap, a[i], a[i];
// Remove all elements from the heap.
for (int i = n - 1; i >= 0; i--)
a[i] = Delete(&heap);
}- 힙 정렬의 전체 시간 복잡도는 O(N * log N) 이다.
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조/C언어] Hash (0) | 2024.06.18 |
|---|---|
| [자료구조/C언어] Sorting Algorithms (정렬 알고리즘) (0) | 2024.06.18 |
| [자료구조/C언어] AVL Tree (0) | 2024.06.18 |
| [자료구조/C언어] Red-Black Tree | 2-3 Tree | B-Tree (0) | 2024.06.18 |
